In the final set of blog posts, lets have a look at how all the changes in MDAnalysis resulted in superior performance of distance based evaluations. In particular, we will look into three different applications (1) Radial Distribution Function (RDF) (2) Identifying Bonds (3) Distance based Selections. Actual Performance comparisons with all the previous commits can be cheked here. Below mentioned benchmarks are local performance comparisons which were made during the incorporation of the code, and some might require a little bit of extra efforts to replicate as the original code will not be in the repository anymore (particularly distance based selections). In any case, I would appreciate to check the commits here to use the previously implemented methods.

RDF

Radial Distribution Function describes the variation of density as a function of distance between two sets of particles. More details on RDF can be found here. RDF is implemented in analysis.rdf module of MDAnalysis, where it builds a sparse matrix of distances and then bins the distances to generate a RDF plot. As discussed before, sparse matrices are fast for smaller datasets but are inefficient in terms of memory and time especially when the size/ number of particles increase beyond 10K in a machine with 4 GB RAM. Therefore, the current implementation fails to calculate RDF for larger dataset. This functionality can be extended by the use of capped_function along with the promise of superior performance than the current implementation. The main gist of rdf calculation lies in _single_frame method in analysis.rdf.InterRDF function:

    
    distances.distance_array(self.g1.positions, self.g2.positions,
                                 box=self.u.dimensions, result=self._result)
    if self._exclusion_mask is not None:
            self._exclusion_mask[:] = self._maxrange

    count = np.histogram(self._result, **self.rdf_settings)[0]

which can be replaced by:

    pairs, dist = capped_distance(self.g1.positions, self.g2.positions,
                                                self._maxrange, 
                                                box=self.u.dimensions)
        
    if self._exclusion_block is not None:
            A, B = pairs[:, 0]//self._exclusion_block[0], pairs[:, 1]//self._exclusion_block[1]
            C = np.where(A != B)[0]
            dist = dist[C]
        
    count = np.histogram(dist, **self.rdf_settings)[0]

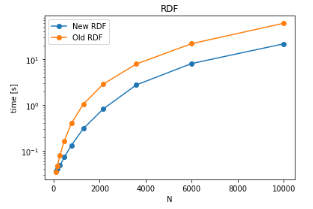
where we first calculate the pairs and distance for each pairs which can be used to construct a histogram. To deal with exclusion blocks, a simple mask using strides in g1, g2 can be used in a way such that if the indices of atom in g1 and g2 are in the multiple of exclusion block indices, they should be ignored. More information about the details and performance can be found in this notebook. The performance is tested against the datafiles (TPR, XTC) which are already present in MDAnalysisTests . Below is the performance of older RDF function and the current implemenation of RDF function which uses capped_distance function.

As can be seen, the performance of RDF has been improved significantly especially for larger set of particles. The x-axis in the graph represents the number of atoms in g1, g2 each. The improvements in time are of the factor of ~ 2-3 for single core computations. However, there might be more improvements possible due to parallellization and SIMD instructions. More discussions on the possible ways to improve RDF calculations can also be found here.

Bonds

One of the important requirement in Analysis of Molecular DYnamics simulations is to be able to distinguish bonds between all the atoms. From an algorithmic perspective, it is a problem of fixed neighbor search where two particles are said to be mutually bonded if the distance between them is smaller than the sum of their individual radius. However, this requires finding neighbors of every atoms, which is time consuming specially when tackled with bruteforce approach. self_capped_distance is an ideal candidate for such applications. The main approach is to identify all the pairs which are within the distance equivalent to the maximum diameter among all the atoms followed by checking the individual distances between them.

    pairs, dist = distances.self_capped_distance(coords,
                                                 max_cutoff=2.0*max_vdw,
                                                 min_cutoff=lower_bound,
                                                 box=box)
    for idx, (i, j) in enumerate(pairs):
        d = (vdwradii[atomtypes[i]] + vdwradii[atomtypes[j]])*fudge_factor
        if (dist[idx] < d):
            bonds.append((atoms[i].index, atoms[j].index))

The notebook with actual benchmarks can be found here, which shows a performance improvement by an order of magnitude for the case under consideration with 8284 bonds. The file used for benchmark is smal.gro and can be found here. Apparently, the factor of time improvement also improves with increase in number of datasets primarily due to the scaling of time complexity of brute force and periodic KDTree/nsgrid.

In this case the time taken by old implementation of topology.guessers.guess_bonds took 3.26 secs, while using capped_function improved the time to 394 ms.

Distance Based Selections

Before capped_distance, distance based selections utilized two different methods _apply_kdtree and _apply_distmat which relied on user’s judgement and required user to have apriori knowledge on both the methods. Distance based selectiion was also memory intensive for PBC calculations as _apply_distmat was enforced for periodic selections. capped_distance deals with these problems in an elegant way by hiding the technical details of the method from the user to focus on the analysis rather than spending time understanding the different algorithms of distance calculations. ‘around’ selection was benchmarked with GRO datafile for the current use case. For the benchmark case of around 5.0 resid 1, previous and current implementation was checked for around selections. The notebook contains the benchmark informations. It can be seen that it took 44 ms with the implemented bruteforce approach for non-PBC calculations. The time can be improved by using KDtree to 37 ms. While the improvement is not that significant with kdtree, nsgrid improves the performance by an order of magnitude. NSGrid took 5 ms for the similar task which is a significant improvement in distance based selections (around a factor of 10).

Overall, three cases which depended on distance evaluations were selected and significant improvement in performance is demonstrated. The next task is to implement capped distance in other distance based analysis such as contact maps, cumulative RDF etc.

Till then, Adios Amigos!!!