Lets begin by reiterating the objectives of the project followed by a bird’s eye view to the approach and finally the quantification of performance improvements in distance evaluations.

The objective of the project is to improve the performance of distance based calculations and their corresponding applications in MDAnalysis. Brute force calculations are highly space inefficient and have a time complexity of O(N^2), which becomes a bottleneck in Molecular Dynamics simulations especially when the size of datapoints is in millions. As discussed before, multiple data structures and algorithms exist which can be more efficient depending on the size and distribution of the datapoints. Binary tree, cell-lists are few among many data structures, which can be used for faster computations to identify nearest neighbours/fixed radius neighbors.

One of the primary aim was to introduce a framework which can automatically select the fastest method based on the size of data, cutoff distance and domain size. This would keep the methods hidden from the user and choose the fastest available method internally, and user doesn’t have to worry about the technical details of the method. However, an extra handle would be provided to the user to override this automatic selection, if desired, and to choose a method of choice. Another advantage of this framework would be an easy extensibility to other faster algorithms/data structures. Addition of another fast algorithm would require just a separate definition and its correspoding rules in one single file and all the applications could reflect the superior performance without much effort.

To introduce the framework, a capped_distance is defined as discussed in previous posts, which takes in query coordinates, search coordinates, cutoff distance as mandatory arguments and min_cutoff, box, and method as optional arguments. Currently method supports bruteforce, pkdtree and nsgrid, which direct to naive brute force implementation, periodic KDTree( a wrapper around scipy.spatial ) and cell-list data structure motivated by GROMACS (more precisely nsgrid.c <https://github.com/gromacs/gromacs/commits/master/src/mdlib/nsgrid.c>_) respectively. To automatically select the method, an internal method _determine_method is used, which includes rules to choose the method. At present, the rules are based on the optimized cutoff distance and size of data points, while in principle, different parameters such as distribution can also be used here. Every method is defined by a separate function, for instance a brute force method inside a capped_distance has same signature as that of capped_distance except the method argument and is defined as _bruteforce_capped as an internal function. Similarly, a self_capped_distance with identical signature is also defined to deal with all the distance evaluations related to all the atoms in the system.

The next step is to optimize individual functions. While one can evaluate the distance matrix, which is fast but limited by sytem memory, another way is to loop over every query and check all the neighbors by searching for neighbors of one query at a time. Even though looping over numpy array is a slower, but this approach is not limited by system memory atleast for the size dealt in MD simulations. However, since we have multiple methods implemented in capped_distance, it would be intuitive to use brute-force algorithm to the limit of system memory and then switch over to other fast methods as a first iteration. Similarly, for KDTree, the current implementation involved using Biopython.KDTree which can be replaced with more stable scipy.spatial. The current implementation of periodic boundary conditions involves looping over every coordinate and evaluating the distance with relevant periodic images to find the minimum distance. As explained in previous post, this operation of looping can be replaced by a more faster cython version, where all the relevant periodic images of particles are concatenated to the original particles. This is followed by a non-periodic search over the new combined dataset which should yield the fixed radius neighbors following Periodic Boudary conditions. This is included in augment_coordinates in lib._augment.pyx in MDAanalysis. Augmenting coordinates also has another advantage which allows easy extensibility to any near neighbor search algorithm to handle Periodic Boundary condition with a little overhead cost. Another method nsgrid which is also discussed in previous blogposts is also added to the capped_distance function.

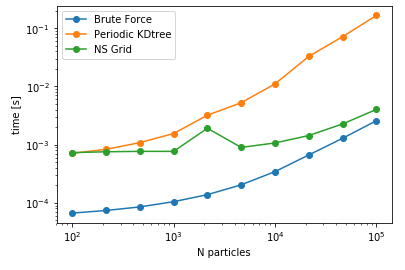
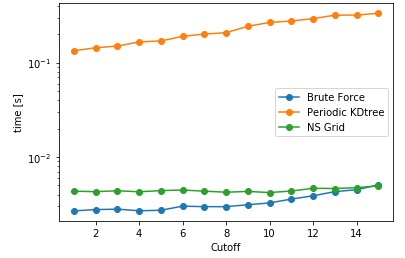
Now moving on to the performance comparisons of these methods, the identified parameters are cutoff distance, datasize, and pbc/no pbc conditions. Almost all of the Benchmarks referred in this blog series can be found here, but the benchmarks for capped_distance can be found in this notebook. Below are few of the important snippets to compare the performances for capped_function with different methods. To begin with, lets compare a single query search for all the implemented methods, its variation with cutoff radius and its sensivity with PBC/no-PBC condition.

Cutoff= 4 units	DataSize = 100K	NoPBC Datasize = 100K

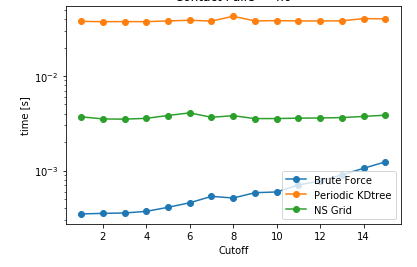As anticipated, bruteforce should be the fastest for this case, as the cost of construction of data structure is larger than querying all the combinations of distances. However, for larger number of queries, the other two methods are expected to be more faster than the naive bruteforce implementation. As a next comparison, lets change the number of query points keeping the size of the data constant i.e. searching varying number of query points against a fixed data set and assess the performance.

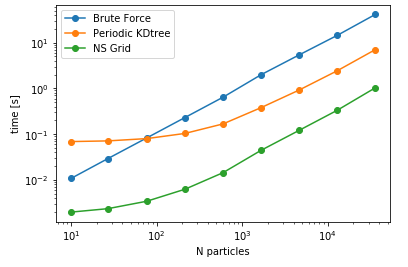
Cutoff= 4 units	DataSize = 100K	NoPBC Datasize = 100K

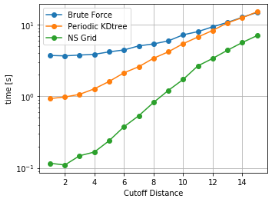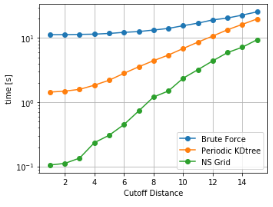
As it can be seen, NSGrid is the fastest for multiple query searches where size is greater than 10 particles. Furthermore, one can contemplate from the trends that NSGrid slows down if the search radius is above a critical value, i.e. greater than 20-30% of the box size in this case.

Another aspect is searching all the particles within a certain cutoff distance, which is defined in lib.distances.self_capped_distance. The performance benchmarks below are for PBC and there is a similar trend for noPBC calculations as well.

Cutoff= 4 units	DataSize = 100K	Datasize = 100K

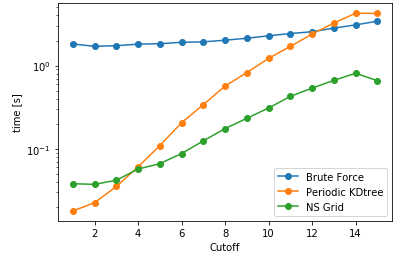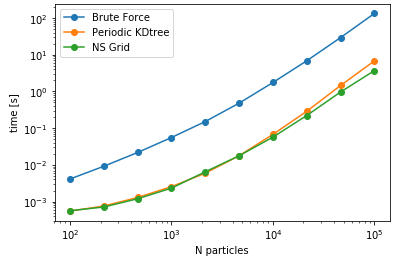
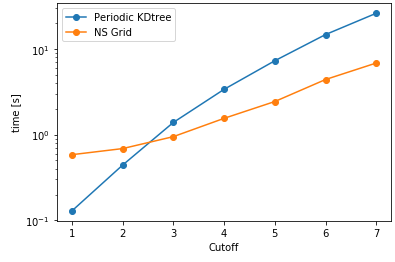
As it can be seen here, PeriodicKDTree shows superior performance, if the desired cutoff distance is below a critical value (typically below 3% of the domain size) and nsgrid becomes superior for larger distances.

The above benchmarks can be used in _determine_method and _determine_method_self to chose the method automatically without user’s intervention. These rules can then be applied for multiple distance based applications in MDAnalysis to gain performance over the previous methods.

The next blogpost will cover the actual improvements for few of the applications in MDAnalysis such as Radial Distribution Function, Distance based selections and identification of bonds in a given dataset. See you there!!