Using Jupyter Notebooks for the first time, and they are awesome!!!

This is the first post after the start of GSoC. A reflection on the past few weeks and summary of the things I have tried, failed and learned should be a good start to this blog.

Journey so far

---

Community bonding period started as soon as the good news arrived, but it ended quickly before I could notice it. Although exams and few other chores also had their fair share in consuming the time. With the remaining time at hand, I focussed on the first part of the project. To give a brief introduction, the project focusses on speeding up the distance calculations, which is one of the fundamental requirement in the MDAnalysis package and Molecular Dynamics Analysis packages in general. More information on the project can be found here.

Over the course of summer, the goal is to identify the suitable candidate for efficient distance calculations. Typically, the number of particles in a Molecular dynamics ranges from few hundred atoms to couple of millions of atoms. The solution to efficient distance based calculations vary significantly based on different factors such as number of particles, their distribution and size of particles. While various data structures exist to handle and manipulate large number of datasets, an efficient solution depends on the problem at hand due to different advantages and disadvantages of these data structures. For instance, for the case of few hundred particles, naive calculation of distances are efficient as opposed to different data strucutures which consume a huge amount of preprocessing time. However, for a relatively large static dataset, it is wise to spend the time in constructing a data-structures to reduce the query times as naive calculations scale with O(N^2) whereas other data structures have query times far lower than the brute force algorithm.

Having discussed the main gist of the project, the remaining blog includes the dissection of the projects into sub-modules which I will be focussing during the course of next few months. Since, at its core, the main problem is the identification of the correct data structure which is robust enough to handle different particle distribution and sizes, the first part of the project is to compare and benchmark different data structures against certain use cases. For the sake of brevity, uniform distribution of point sized particles are selected to be used, unless specified, for the benchmark studies. Two main use cases are identified for distance calculations, which can be listed as follows :

• Typically selections of atoms form a major class of problems required in the analysis of MD trajectories. An around distance selection statement like around protein 3.5 selects all the atoms not beloning to the protein within a distance of 3.5 units from the protein particles. As a use case, we consider selection of all the particles within a certain distance from a query point.
• Another major class which depends heavily on distance calculations is the evaluation of all possible pairs of particles within a definite distance from each other. While this forms the crux of the problem, similar analysis like contact maps, bond formation also form the subset of this problem.

Based on the above description, one might think selection use case as a subset of pair calculations such that similar query operation is executed for every particle. While it is correct, but due to large number of computations involved in pair distance evaluations, a small modification in accessing the particles might lead to a significant change in overall time. For instance, in a hierarchical tree based structure, every query operation needs to traverse the tree to find its position within the tree which itself is time consuming. If the time to find the position can be made independent of the number of particles, this seemingly small modification leads to huge reductions in total time.

Since the solution revolves around different data structures, it is best to list down different data strcutures and their current state. While doing so, it should also be kept in mind that a typical boundary condition frequently used by Molecular dynamics community, Periodic boundary conditions, should be supported by the data structure.

• Naive Distance - This is not a data structure, per se, but a method to evaluate the distances and is already implemented in MDAnalysis. The algorithmic running time for this is O(N^2) and more so the space complexity also scales with O(N^2) if distance between all the particles are evaluated. Furthermore, the algortihm allows easy implementation of periodic boundary condiions.
• Grid Structures - These are linear data structures, where the domain is divided into linear grids. Preprocessing time for this data structure scales as O(N), as every particle is alloted a cell in the grid. For distance calculations, only the particles in the neighbourhood are used for distance evaluations. This specific step reduces a huge amount of time. The query time for such data structure is also dependent on the distribution of particles as opposed to independent naive distance calculations. The query time for nearest neighbour for this class of data structure is independent of the number of particles, provided the particles are arranged in a sorted array. For the case useful for MDAnalysis, the query time for an around selection depends on the number of particles in every cell i.e. depends on the density of particles irrespective of the number. Another factor which affects the performance is the cellsize. Smaller the cell size, higher is the cell checking with very low number of cells actually having a particle whereas large size of cell tends to perform poorly and close to naive distance algorithm. Typically, a cellsize equivalent to cutoff radius is used, which is classified as cell-list algorithm. Various algorithms exist for grid structures. Some of them are Cell-list, Combined cell-list and verlet, Full-list, twin grid, excelfile etc. An excellent review is provided here. A particular advantage of this method is easy parallellization and independent query time along with linear scaling for construction time. Due to these advantages, cell-list combined with verlet is generally used in Molecular dynamics codes. However, the advantage of verlet lists is pronounced in dynamic data sets, when the atom position donot change much in consecutive data sets. For MDAnalysis, these advantages become less pronounced due to static datasets and therefore this algorithm is not pursued further. Due to the similarity to naive distance calculations, this data structures also allows easy implementation of Periodic boundary conditions.
• Tree Structures - Some of the often used tree structures are KDTree, Octree and R-tree. KDtree is a bindary tree which is often used for high dimensional searches. KDtree is a space partitioning data structure for organizing points in a k dimensional space. Typically, these are used for range searches and near neighbour searches in k dimensional space. For the requirements of MDAnalysis, KDtree has been implememented to generate tree structure in 3 dimensions. As opposed to a typical tree, where every leaf node corresponds to a single atom, leaf node in a current implementation can hold a list of particles. This step significantly reduces the time of distance calculations from a query for both fixed radius and nearest neighbour searches. More information on KDtree can be found here. Tree structure usually require huge amount of construction time which scales as O(NlogN) for a bucket size of 1. The time changes with the bucket size as well and typically a bucket size of 10-30 particles is preferred. Query time for KDtree scales with O(logN), where most of the time is spent in traversing the tree to locate the node of query point. Implementation of periodic boundary conditions is little tricky in tree-structures. However, it is already implemented in MDAnalysis. Octree is another structure which is based on recursive division of a cube into its eight octants. This structure shares the same advantages and disadvantages of KDtree. While KDtree is a good choice for manipulation of high dimensional datasets, octree is specifically suited for three dimensional dataset. Due to an organized structure, accessibility of different nodes in faster in this structure. However, since every node has eight childs with each child having equal probability of containing the query point, the query time is dependent on the order of tree traversal. Inspite of the clear advantages of Octree over KDtree, I didn’t come across any implementation of periodic boundary conditions in OCtree. It is more likely that the scaling of Octree will follow a similar trend to the periodic implemetation of KDtree. The construction time for OCtree scales as O(N) and query time scales as O(klogN), where k depends on the number of particles in each cell and total number of bins. More information on Octree can be found here.

Regarding the current status of different data structures, the brute force/ naive distance algorithm currelty resides in MDAnalysis.lib.distances, which is parallellization enabled as well as pbc aware. In terms of grid structure, a pure python implementation is used in GNM module of MDAnalysis, a CellGrid package also offers a python implementation of cell-list structure. Another package of fast distance calculations based on the cell-list data structure resides in FATSLiM package. More information can be found here. All the mentioned cell-list structures are PBC aware. KDtree is also implemented in MDAanlysis, which is PBC aware and sits in MDAnalysis.lib.pkdtree. Octree is not implemented to handle periodic boundary conditions (PBC), but a fast implemetation for non-PBC is implemented in Point Cloud Library (PCL). Other than these, non PBC KDtree data structures are also implemented in Biopython and Scipy.

The task now is to analyze the methods and their suitable applications. The plan is to provide benchmarks for different use cases and establish the best and robust method for distance evaluations. Although there might not be a single method to serve this purpose, another goal is to assess the limiting conditions when one method becomes superior over the other in terms of performance. The tasks can be dissected into following mini-tasks:

1. Benchmarks for build and query time for single queries.
2. Benchmarks for pair contacts for bond analysis.
3. Benchmarks for KDtree to compare Scipy, Biopython and current implementation of Periodic KDtree.
4. Relevant benchmark for Octree and cython implementation of Nearest neighbour search implemented in FATSliM.
5. The cellgrid module in MDAnalysis is not optimized in terms of grid size and cutoff distances. The next task is to optimize the Cellgrid API and Benchmark it against the previous cases.

Benchmark Studies

---

Here, I present the initial benchmarks, a condensed version of conclusions that can be derived from initial benchmarks is also presented. For all the studies presented below, I am using Intel Core i5-5200 processor clocked at 2.20 GHz and RAM of 8GB. The related ipython notebooks are available here. To collect the timings, an inbuilt magic method timeit is used. For any function timeit can be used as %timeit function(arguments) in ipython notebook. Similarly, for memory details, memit magic method is used here.

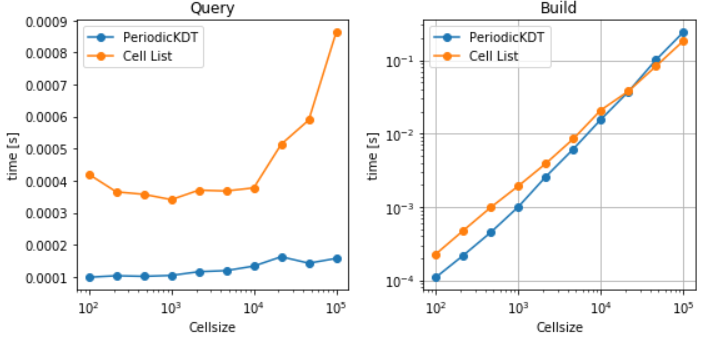
• For Build and Single query timings related to different data structures (particularly, Cellgrid, PeriodicKDTree, KDTree Scipy, and pure python implementation of Cell-list) are used here for benchmarks. For single point queries, it can be concluded that both the query and build time are larger for the case of Cell-list case shown here. However, it is anticipated that an efficient implementation of cell-ist should consume less time as opposed to KDtree for single point query.

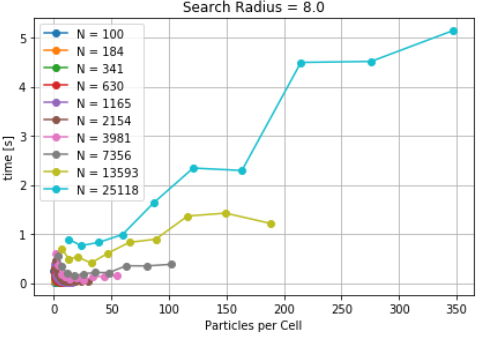
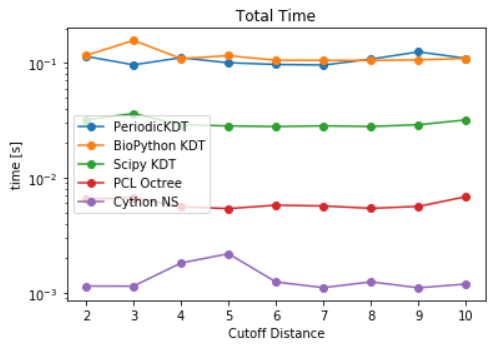
• For pair contacts, naive distances, KDtree and Cellgrid packages are used for the benchmarks. For the sake of parametric study, a cutoff distance of 10 units is chosen i.e the motive is to time different functions to find all particle pair within a distance of 10 distance units. For naive distances, self_distance_array, as implemented in MDAnalysis is used which constructs an array and stores the distance of each pari of particles, one at a time. This causes sudden increase in memory usage which is also documented here. Timings for differetn cutoff radius are also noted to increase with increase in cutoff distances for a fixed number of particles. The goal, here, was to characterize the CellGrid package against already implemented techniques. It also involves the variation of time due to different cutoff radius. It is observed that smaller cutoff distance consumes a huge amount of time. Since, cellsize is other parameter which controls the time. A more interesting question was whether a significant reduction in timing can be achieved by increasing the cellsize for a given cutoff distance. As a result, density was identified as a parameter and particles per unit cell was optimized for lower calculation time. The difference in time was found to be significant for small number of particles. A particle density of 30 particles per cell is identified as an optimized parameter (see here). The time for optimized cutoff was also compared against tree structures, but KDtree took less time than the optimized Cellgrid method.

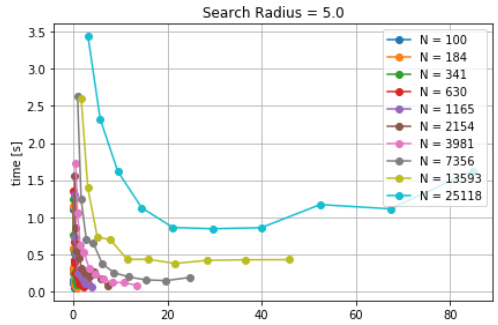
• A use case of selections with different particle type and distribution also needs to be checked. As most of the MDAnalysis community requires selection of one group of particles around another group of particles. Two different geometries i.e. Slab distribution and spherical protein with solvent distribution are chosen for benchmark studies. For spherical protein particle surrounded by a solvent, KDtree aced among the cellgrid and brute force method for large number of particles. (see here.

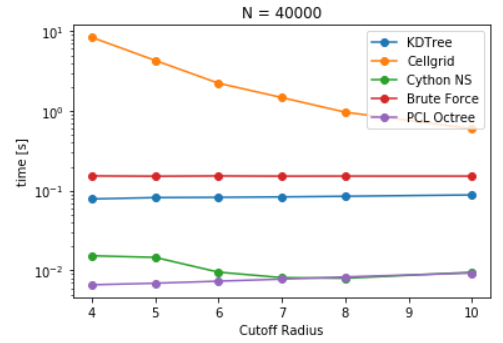
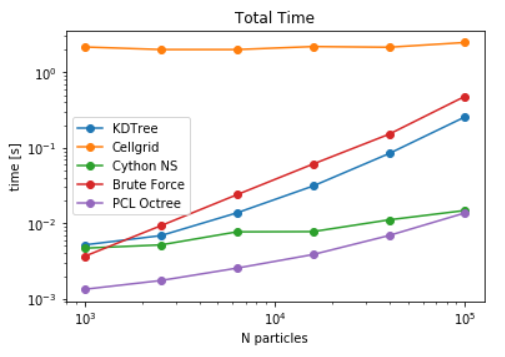
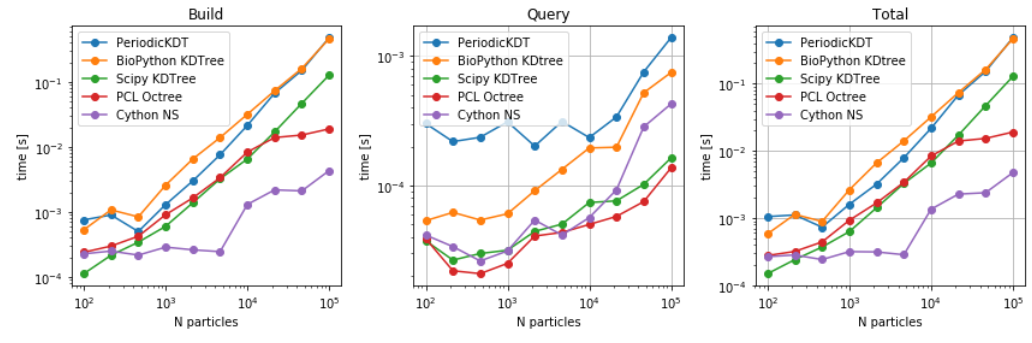
• Single queries are benchmarked against non-PBC and PBC aware methods by choosing the query point deep inside the box such that periodic images are never required for computations in any of the methods. Here, Octree and cython based neighbour search method is also used for benchmarking. The library implemented in FATSLiM showed the fastest build and query time for large number of particles. However, for small number of particles, non-periodic octree evaluated the selections in shortest time.(see here). Similarly, spherical selection was also evaluated for all the data structures. As anticipated, Octree and Neighbour search in FATSLiM shows the best performance(see here).

Based on these benchmarks, it can be concluded that Neighbour search (FATSLiM) and Octree are definitely good alternatives to reduce the time of distance calculations. Although it was not possible to evaluate the pair contacts of all the particles using octree, but the scaling can be anticipated to be similar to the periodic KDTree.

All this for now. See you in the next blog post.